ウェーブレット行列で、先頭からの検索を速くする
（注：今回の内容は元論文に書いてあったわけではないので独自研究気味です）
前々回と前回で、ウェーブレット行列を使ったアルゴリズムを二つ紹介しました。
二つとも、ある配列に対して開始位置と終了位置を指定した範囲についての操作です。
RankLessThan(), QuantileRange のどちらも、開始位置と終了位置が各レベルでどこになるのかを調べるために、1レベルあたり 2回、ビット列に対して rank() （ある位置より左に 0 または 1 がいくつあるか）という操作が必要でした。
これは十分効率的なのですが、実際に使う時には、配列の先頭を開始位置として、終了位置だけを指定するというケースが多くあります。話題のwat-arrayを使ってBurrows-Wheeler変換(BWT)してみた - EchizenBlog-Zwei で紹介されている Burrows-Wheeler 変換で使われるのも、先頭からの RankLessThan() です。先頭から検索する時だけでも、少し速く実行できたらうれしいですよね。
そのために、先頭から検索をする場合に、範囲の開始位置がどのように移動するかを覚えておくことを考えます。
まず、最初のレベルでの開始位置は 0 です。その後、最上位ビットが "0" か "1" かによって、次のレベルでの開始位置が変わります。"0" の場合と、"1" の場合の開始位置を覚えておきます。
それぞれの次のレベルでも、最上位ビットが "0" か "1" かによって、その次のレベルの開始位置が変わります。ですので、「最上位ビットが "0" で、2番目のビットが "0" の場合」「最上位ビットが "0" で、2番目のビットが "1" の場合」「最上位ビットが "1" で、2番目のビットが "0" の場合」「最上位ビットが "1" で、2番目のビットが "1" の場合」の 4通りについて、それぞれ次のレベルで開始位置がどうなるかを覚えておきます。
このように、それぞれのレベルで、覚えておくべき開始位置が 2倍に増えていきます。ここまで使ってきた例では、配列の中に出てくる数が 16通りで、レベルが 4つなので、1レベル目で 2個、2レベル目で 4個、3レベル目で 8個、4レベル目で 16個になります。つまり 2+4+8+16=30個で、16の 2倍以下です。一般的なテキスト処理では、出てくる数は 1バイトで表せる 256通り（日本語などの場合も、UTF-8 などでバイト単位で扱うことが多い）なので、覚えておくべき開始位置の数は 256 の 2倍ぐらいと、たいした量にはなりません。
これまで例として使ってきた配列の場合、各レベルで開始位置がどのようになるかを見てみます。
まず、1レベル目では開始位置は 0 です。
全体で "0" の数は 19個なので、最上位ビットが "1" の場合は、次のレベルでの開始位置が 19 になります。"0" の場合は 0 のままです。
2レベル目では、そのそれぞれの場合について、上から 2ビット目が "0" か "1" かによって 3レベル目での位置を計算します。"0" の場合は、今の位置より左にある "0" の数を数えます。"1" の場合は、今の位置より左にある "1" の数を数えて、それを真ん中の「0-1 境界線」の位置に足します。これは、検索をする場合と同じです。
計算すると、上位 2ビットまでの数字によって、開始位置は次のようになります。
上位 2ビットが 00, 10, 01, 11 の順に並びます。ビットの並びを逆にしたもの（00, 01, 10, 11）を配列の添字として使うと扱いやすくなります。
同じように、3レベル目が "0" か "1" かによって、4レベル目の位置を決めます。計算すると、次のようになります。
やはり順番は 000, 100, 010, 110, 001, 101, 011, 111 となり、ビットの並びを逆にしたものの順番になります。例としている配列の中に偶然 8 と 9 がなかったので、上位 3ビットが 100 のところが空になっています。
4レベル目では、仮想的なもう一つ下のレベルを考えて、そこでの位置を決めます。次のようになります。
これは、ウェーブレット木でできることはウェーブレット行列でもできるで導入したものと同じです。
例として、配列の先頭からインデックス 24 までの範囲に、「11 より小さいもの」「11 そのもの」「11 より大きいもの」がそれぞれいくつあるかを調べることを考えます。
最初のレベルでは、検索範囲は次のようになっています。
11（2進数で "1011"）の最上位ビットは "1" です。いつものように、次のレベルでの終了位置を決めます。青線より左にある "1" の数（10個）の分、「0-1 境界線」から右に移動した位置になります。
開始位置は、あらかじめ保存しておいたテーブルを使います。最上位ビットが "0" か "1" かによって、検索開始位置はそれぞれ次のようになります。
これによると、インデックス 19 で、「0-1 境界線」と同じになります。図で範囲を示すと、次のようになります。「0-1 境界線」と開始位置の赤線が重なるので、茶色で示しています。
11（2進数で "1011"）の 2ビット目は "0" です。次の終了位置は、青線の左にある "0" の数を数えて決めます。11個あるので、インデックス 11 になります。
開始位置は、またテーブルを参照します。それによると、開始位置は次のようになっています。
上位 2ビットは 10 なので、開始位置のインデックスは 7 になります。図で範囲を示します。
11（2進数で "1011"）の 3ビット目は "1" です。次の終了位置は、青線の左にある "1" の数（6個）の分、「0-1 境界線」から右の位置になります。
開始位置のテーブルは次のようになっています。
上位 3ビットは 101 なので、開始位置はインデックス 16 になります。図で示すと、次のようになります。
4ビット目は "1" です。終了位置を同じように決めます。インデックス 26 になります。
開始位置は、またテーブルを参照します。
1011 なので、インデックス 23 です。最終的な範囲は次のようになります。
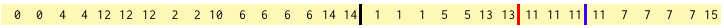
これで、範囲内で 11 の出現回数が 3回だということがわかります。検索キーより小さい数と大きい数を数えるところは今回は省略しましたが、ウェーブレット行列による RankLessThan() と同じです。
ところで、RankLessThan() はこういう名前で代表させていますが、これまで説明したようにキーより小さいもの・キー自体・キーより大きいものの数は一度にわかります。これを配列の先頭から実行する場合、各レベルごとに 1回だけ、簡潔ビットベクトルに対する rank() の呼び出しが発生することになります。これは十分速いため、Rank() という関数を別に実装する必要はありません。また、開始位置を指定する関数を実装する必要もありません。先頭からの終了位置までの結果と、先頭から開始位置までの結果の差分をとることで求められます。
QuantileRange() でも、先頭からの場合は、同じようにレベルごとに 1回だけの rank() 呼び出しで実行できます。ただ、この場合は開始位置と終了位置を指定するインターフェースが必要になります。先頭から開始位置までの結果と、先頭から終了位置までの結果を合わせても、開始位置から終了位置までの結果を知ることはできないからです。私のテスト実装では、開始位置と終了位置を指定したインターフェースで、開始位置が先頭の場合のみ表を参照して高速化するようにしています。
文字の種類が多い場合、開始位置を覚えておく領域が問題になることがあるかもしれませんが、これは先頭からの検索を高速化するためのものなので省略できます。
ウェーブレット行列に関する記事は、とりあえずここまでで一区切りにします。Select() については書いていませんが、私のテスト実装 にはあるのでご参照ください。
ウェーブレット行列をえちぜんさんの紹介記事で知り、その感動で一気に書きました。
ウェーブレット木は実装が複雑だったので手が出ないでいたのが単純になって喜んでいたのですが、ちょっと考えると、先頭からの検索を高速化しようと思うと結局ウェーブレット木のノードにあたる情報を持っておかないといけないのでがっかりしました。先頭という位置を特別扱いしなければいいのですが、実際に使う時は先頭からの検索が多いので、やはり必要なのではないでしょうか。
そういえば、ウェーブレット木のほうでは、記号ごとの出現回数を効率的に保存するということをしていますが、ウェーブレット行列のほうではそんなに必要性がないんじゃないのかなぁと思います。これを使うと、各レベルでの開始位置を記憶しないでも Select() を速くできる（簡潔ビットベクトルに対する select() 呼び出しを、レベルごとに 2回ではなく 1回にできる）という利点はあるのですが、他の関数には使えません。開始位置を記憶する領域はないけれど、出現回数を圧縮して保存するための領域ならちょうどあって、Select() だけでいいから速くしたい、という状況はあまりないような気がします。文字数が少なければ各レベルで開始位置を記憶、多ければ記憶しないというのでいいのではないでしょうか。
