今回は、可変次数 CRF の計算方法についての解説。
これはぼくの研究で、2年前に修論にして、国内の言語処理学会にも出したのだが、一人で国際学会に出せるような論文にするまでのモチベーションが湧かず、そのままになっている。
一緒に考えてくれる人を募集中。
まず、可変次数 CRF について。
可変次数 CRF という考え方自体は新しいものではなく、Conditional Random Fields with High-Order Features for Sequence Labeling(Nan Ye et al., 2009) でも紹介されている。
CRF*1 では、一般的な素性関数の形は次のように表せる。
この形では、たとえば「前の前のラベルが A で、今のラベルが B の時に 1 になる」といった、ラベル列をスキップした素性関数なども定義できることになる。
だが、可変次数 CRF ではそのような素性関数は扱わず、文脈に関する条件と連続したラベル列に関する条件を組み合わせたものを素性関数とする。
たとえば、次のようなものは、可変次数 CRF の素性関数となりうる。
- 前のラベルが N で、今のラベルが N の時に 1 になる
- 前の単語が "ed" で終わり、今のラベルが N の時に 1 になる
- 今の単語が "s" で終わり、前の前のラベルが A で、前のラベルが N で、今のラベルが V の時に 1 になる
ここで注意が必要なのは、次の点。
- 文脈に関する条件はなくてもいい。その場合、常に 1 になるような文脈に関する条件と、ラベルに関する条件が組み合わされていると解釈できる。
- ラベルに関する条件は必ず存在する。なぜかというと、ラベルに関する条件がないような素性関数はすべてのラベル列に対して同じ値をとるため、判別モデルである CRF では役に立たない。
- 文脈に関する条件としては、どの位置の単語を使ってもよい。いずれにしても、ある位置で文脈に関する条件が満たされるかどうかは一意に決まる。
前回と同じく、可能なラベルが N, V, A の三つで、単語列は "time flies like" であり、素性関数が次の 5 つである場合を考える。
- 文脈にかかわらず、今の位置でラベルが "N" の時に 1 になるもの。重みは 2。
- 文脈にかかわらず、今の位置でラベルが "V" の時に 1 になるもの。重みは 3。
- 文脈にかかわらず、今の位置でラベルが "A" の時に 1 になるもの。重みは 5。
- ある位置の単語が "es" で終わり、その前の位置のラベルが "N" で、今の位置のラベルも "V" である時に 1 になるもの。重みは 2。
- ある位置の単語が "like" であり、その前の位置のラベルが "V" で、今の位置のラベルが "A" である時に 1 になるもの。重みは 3。
すると、前回見たように、それぞれのラベル列のスコアは次のようになる。
N-N-N: 8 N-N-V: 12 N-N-A: 20 N-V-N: 24 N-V-V: 36 N-V-A:180 N-A-N: 20 N-A-V: 30 N-A-A: 50 V-N-N: 12 V-N-V: 18 V-N-A: 30 V-V-N: 18 V-V-V: 27 V-V-A:135 V-A-N: 30 V-A-V: 45 V-A-A: 75 A-N-N: 20 A-N-V: 30 A-N-A: 50 A-V-N: 30 A-V-V: 45 A-V-A:225 A-A-N: 50 A-A-V: 75 A-A-A:125 合計:1420
そして、それぞれの素性関数のスコアは以下の通り。
- 文脈にかかわらず、今の位置でラベルが "N" の時に 1 になるもの: 792
- 文脈にかかわらず、今の位置でラベルが "V" の時に 1 になるもの: 1428
- 文脈にかかわらず、今の位置でラベルが "A" の時に 1 になるもの: 2040
- ある位置の単語が "es" で終わり、その前の位置のラベルが "N" で、今の位置のラベルが "V" である時に 1 になるもの: 240
- ある位置の単語が "like" であり、その前の位置のラベルが "V" で、今の位置のラベルが "A" である時に 1 になるもの: 540
これは、アルゴリズムの検算に使える。
合計・差分アルゴリズムでは、それぞれの素性関数のスコアと全ラベル列の合計スコアを動的計画法で求める。
前者を後者で割ることによって素性関数の期待値が求められ、それによってパラメータを訓練データの尤度を大きくするものに更新できる。
考え方としては、次の記事で紹介する前向き・後ろ向きアルゴリズムと同じように、前方向からと後ろ方向からのスコアを計算をするのだが、違うところも多い。
一番違うのは、「エッジ」と「ノード」で構成されるグラフにならないということ。
しかし、ここでは便宜的に「ノード」という用語を使うことにする*2。
前向き・後ろ向きスコアは、それぞれ「先頭からそのノードまでのスコアの合計に、そのノードの重みを掛けたもの」、「最後尾からそのノードまでのスコアの合計」とする。つまり、後ろ向きスコアにはそのノードの重みを掛けない。
そして、それぞれについて、合計と差分のスコアをそれぞれ求める。
合計スコアは、先頭・最後尾からそのノードに至るまでのすべてのスコアを合計したもの。
差分スコアは、先頭・最後尾からそのノードに至るまでのすべてのスコアと、その接尾辞ノード(後述)のスコアの差分。
どうしてこの 2 つを使うのかという説明は難しいけれど、こうすることによって計算ができる。
以下では、合計・差分アルゴリズムを使って、上の例でのそれぞれのスコアを求める過程を示す。
まず、前向きの段階。
最初の位置では、"N", "V", "A" というノードができ、それぞれで 1 になる素性関数の重みは 2, 3, 5 なので、これをそのまま前向き合計スコアとする*3。
ここで、「ラベル列なし」というものに対応するノードを一つ導入し、それを ε とする。これは、次の位置について考える時に必要になるもの。これの前向き合計スコアは、"N", "V", "A" のスコアを合計したものとする。すると、次のようになる。
そして、2番目の位置。
ここでは、"N-V" というラベル列を持つ素性関数があるので、それ用のノードを別に作る。
そして、ここで「前の列から引き継ぐスコア」を計算する。
引き継ぐ元は、今のノードのラベル列から末尾をひとつ取り去ったラベル列を持つ左ノード。今後、対応する左ノードと呼ぶ。
まず、N のノード。
N のノードはラベル列の長さが 1 なので、末尾をひとつ取り去ると空になる。
よって、引き継ぐ元は前の列の ε になる。
2 列目の N のノードのスコアは、N-N, V-N, A-N の合計になればいい。それらの遷移には、どれにも素性関数が割り当てられていないので、N に入る 1 列目のスコアは (N+V+A) になる。それが、ε のスコアとなっている。
次のノードは N-V。
N-V の末尾を取り去ると N になるので、前の位置の N からスコア 2 を引き継ぐ。
ここで気をつけないといけないことがある。
2 列目が V であるもののうち、1列目が N のものは、N-V のノードのスコアになり、V のスコアにはならないということ。
重複して計算しないように、N-V の段階で、自分が引き継ぐ分を V から引いておく。
次のようになる。
引く対象は、一般的には「自分のノードのラベル列の接尾辞となるようなラベル列を持つノード」になる。そういうノードを接尾辞ノードと呼ぶことにする(もっとも、そういうノードは複数ありうる。その中で最長のものを選ぶことになるため、厳密には最長接尾辞ノードになるが、ここでは接尾辞ノードと呼ぶ)。
次が V のノード。N のノードと同じく、対応する左ノードは ε。
前の列のノードが N である分は N-V に行くので、それはあらかじめ引いてある。
結果として、次のようになる。
これは、(N+V+A) から N を引いたものなので、(V+A) ということになる。
A のノードも、対応する左ノードは ε になり、10 点をそのまま引き継ぐ。
ここで、それぞれのスコアにノードの重みを掛ける。
N-V のノードでは、次の二つの素性関数が 1 になるため、ノードの重みはそれらの重みを掛け合わせた 6 になる。
- 文脈にかかわらず、今の位置でラベルが "V" の時に 1 になるもの。重みは 3。
- ある位置の単語が "es" で終わり、その前の位置のラベルが "N" で、今の位置のラベルが "V" である時に 1 になるもの。重みは 2。
その他は、それぞれで 1 になる素性関数の重みである 2, 3, 5 となる。
重みを掛けると、次のようになる。
ここまでで計算したスコアは差分スコアであり、たとえば N-V のノードのスコアと V のノードのスコアは別になっている。
ここで、合計スコアを別に求める。
次の列にスコアを引き継ぐ時、たとえば N-V のノードと V のノードは両方とも 2列目のラベルが V であるという共通点があるため、それらのスコアをまとめておく必要がある。そして、3 列目で V-A の計算をする時には、V の合計スコアを引き継ぐことになる。
合計スコアを求めるには、各ノードの差分スコアを、自分の接尾辞ノードの差分スコアに足していけばいい。
まず、N について考える。差分スコアを自分の合計スコアとして、それを接尾辞ノードである ε の合計スコアに足す(一列目同様、ε というノードを作る)。
N-V では、接尾辞ノードは V になる。差分スコアを自分の合計スコアとして、それを V に加える。
V では、自分の差分スコアを合計スコアに足して、その結果を接尾辞ノードである ε の合計スコアに足す。
A でも同じようにする。
次は 3 列目。
ここでは、V-A のノードがあるため、ノードは次のようになる。
N は、対応する左ノードである ε のスコアを引き継ぐ。
V も同じ。
V-A の対応する左ノードは V なので、そのスコアを引き継ぐ。また、その分は接尾辞ノードである A のところから引く。
そして、A のノード。
V-A の分はあらかじめ引かれている。A のノードは、対応する左ノードである ε のスコアを引き継ぐ。
それぞれのノードの重みを掛ける。
V-A の重みは、
- 文脈にかかわらず、今の位置でラベルが "A" の時に 1 になるもの。重みは 5。
- ある位置の単語が "like" であり、その前の位置のラベルが "V" で、今の位置のラベルが "A" である時に 1 になるもの。重みは 3。
を掛け合わせたものになるので、15 になる。
それ以外は、1 列目や 2 列目と同じ 2, 3, 5 になる。
3列目についても、それぞれの合計スコアを求める。
N のノードでは、ε に自分の合計スコアを足す。
V でも同じ。
V-A では、自分の合計スコアを接尾辞ノードである A に足す。
A では、自分の差分スコアを合計スコアに足し、それを接尾辞ノードである ε に足す。
3列目の ε の合計スコアは、上で全パターンを網羅して調べた合計スコアである 1420 と一致していることが確認できる。
ここまでで求めたのは、各ノードの前向き差分スコアと前向き合計スコアということになる。
しかし、たとえば 2 列目の N-V のスコアは、前向きスコアだけでは求められない。後ろ向きスコアを掛ける必要がある。
ここからは、後ろ向きの段階について。
前向きスコアは、そのノードの重みを掛けたものとしている都合上、後ろ向きスコアは、そのノードの重みを掛けないものとする。
そうすると、3 列目はすべて 1 になる。これは、ここでは後ろ向き合計スコアと呼び、後で出てくる後ろ向き差分スコアと対になる。
後ろ向き合計スコアとは、そのノードより後ろのものから引き継いだ点数の合計。3 列目は最後尾なので、すべて 1 となる。
まず、それぞれのノードについて、ノードの後ろ向き合計スコアにノードの重みを掛ける。(重みを掛ける前の後ろ向き合計スコアは後で使うので、別に保存しておく)。
それから、下から順番に、自分のスコアを対応する左ノードに足していく。
A の対応する左ノードは ε になる。スコアの 5 を足す。
V-A のノードでは、V-A のスコア 15 から、接尾辞ノードである A のスコア 5 を引いて、それを対応する左ノードである V の差分スコアに足す。
最後が V で終わるノードでは、右列のラベルが A であるところのスコアが、 A ではなく V-A のものになるので、その差分を記録しておくという解釈。
次の V では、接尾辞ノードは ε なので、そのままスコア 3 を左の ε に足す。
N でも同じ。
ここまでで出たのが、2列目の各ノードの後ろ向き差分スコア。
これを足し込んでいくと、各ノードの後ろ向き合計スコアが計算できる。
具体的には、各ノードで、その接尾辞ノードの合計スコアに自分の差分スコアを足していくことになる。
2列目のノードを下から順番に見ていく。
ε のノードは接尾辞ノードがないので、差分スコアがそのまま合計スコアになる。
A のノードは ε が接尾辞ノードになる。差分スコアは 0 なので、ε の合計スコアがそのまま A の合計スコアになる。
V のノードも ε が接尾辞ノードだが、自分の差分スコアが 10 なので、ε の合計スコアと足し合わせて 20 になる。
N-V のノードは、V が接尾辞ノード。差分スコアは 0 なので、V の合計スコアがそのまま N-V の合計スコアになる。
N のノードは ε が接尾辞ノードで、差分スコアは 0。ε の合計スコアそのままになる。
これで、2 列目の後ろ向き合計スコアがすべて求められた。
次は、もう一度 2 列目に注目して、1 列目の差分スコアを求める。
まず、2 列目の ε を除く全ノードについて、それぞれの後ろ向き合計スコアに重みを掛ける(ε は左ノードにつながらないので無視する)。
まず、A のスコアである 50 を、対応する左ノードである ε の差分スコアに足す。
次に、V のスコア 60 を ε の差分スコアに足す。
N-V では、自分のスコア 120 から、接尾辞ノードである V のスコア 60 を引いた差分を、対応する左ノードである N に足す。
N では、自分のスコア 20を対応する左ノードである ε の差分スコアに足す。
これで、1 列目の差分コストが求められたので、1 列目の各ノードに注目して合計スコアを求める。
ε は、接尾辞ノードがないので、合計スコアは差分スコアに等しくなる。
A では、差分スコアが 0 なので、接尾辞ノードである ε の合計スコアがそのまま合計スコアになる。
V でも同じ。
N は、差分スコアが 60 なので、接尾辞ノードである ε の合計スコアと足した 190 が合計スコアになる。
これで、各ノードの前向き・後ろ向きの合計・差分スコアが求められた。
前向きの差分スコアと、後ろ向きの合計スコア(ノードの重みを掛ける前のもの)を掛け合わせると、各ノードのスコアが求められる。それぞれ、次のようになる。
それぞれの位置でのスコアを合計すると、どこでも 1420 になっていることがわかる。
しかし、ここでひとつ気をつけることがある。
ノードとしては N-V と V、V-A と A を分けているが、N-V では「ラベルが V の時に 1 になる素性関数」も 1 になり、V-A では「ラベルが A の時に 1 になる素性関数」も 1 になる。
このことを考え、接尾辞ノードが ε でないそれぞれのノードについて、自分のスコアを接尾辞ノードのスコアに足し込む。
これを元に、それぞれの素性関数の合計スコアを求める。
すると、次のような結果になる。
- 文脈にかかわらず、今の位置でラベルが "N" の時に 1 になるもの: 380+200+212=792
- 文脈にかかわらず、今の位置でラベルが "V" の時に 1 になるもの: 390+720+318=1428
- 文脈にかかわらず、今の位置でラベルが "A" の時に 1 になるもの: 650+500+890=2040
- ある位置の単語が "es" で終わり、その前の位置のラベルが "N" で、今の位置のラベルが "V" である時に 1 になるもの: 240
- ある位置の単語が "like" であり、その前の位置のラベルが "V" で、今の位置のラベルが "A" である時に 1 になるもの: 540
と、すべてのパターンを網羅して計算した結果と一致する。
流れをまとめる。
まず、準備段階。
- それぞれのノードで 1 になる素性関数の重みを掛け合わせる。
- それぞれのノードの重みに、接尾辞ノードの重みを掛ける。
前向きステップでは、一列ごとに次の処理をする。
- それぞれのノードについて、前の列の対応するノードから合計スコアを引き継ぐ。接尾辞ノードが ε でなければ、自分が引き継いだ合計スコアを接尾辞ノードから引く。
- それぞれのノードについて、1 で求めたスコアにノードの重みを掛け、それを前向き差分スコアとする。
- それぞれのノードについて、接尾辞ノードの前向き差分スコアに自分のものを足し込み、前向き合計スコアとする。
後ろ向きステップでは、一列ごとに次の処理をする。
- それぞれのノードについて、自分の後ろ向き差分スコアに接尾辞ノードのものを足し込み、後ろ向き合計スコアとする。
- それぞれのノードについて、後ろ向き合計スコアにノードの重みを掛ける。
- それぞれのノードについて、前の列の対応するノードに 2 のスコアを引き継ぐ。接尾辞ノードが ε でなければ、自分の 2 のスコアから接尾辞ノードのものを引いたものを引き継ぐ。
また、これらの前に、各ノード列を構築し、それぞれのノードについて「対応する左ノード」と「接尾辞ノード」を調べておく必要がある。
この計算方法を使うと、系列の長さが倍になっても、計算量は倍になるだけですむ。
また、「各列で文脈に関する条件を満たす素性関数」についてだけ考えればいいため、次数が増えても計算量が爆発しない。
上での例では、素性関数の次数は最高で 1 次であるため、普通の前向き・後ろ向きアルゴリズムでも計算ができる。
合計・差分アルゴリズムの特色である、高次の素性があっても計算量が爆発しないという利点を見るために、上の例に次の素性関数が加わった場合を考える。
- ある位置の単語が "like" であり、その前の前の位置のラベルが "N" で、前の位置のラベルが "V" で、今の位置のラベルが "A" である時に 1 になるもの。重みは 0.5。
この設定ですべてのラベル列のスコアを再計算すると、合計スコアは 1330 になる。
この場合、スコアの計算がどのようになるかを見てみる。
前向きの段階では、3 列目の V のノードまでは上での例と同じになるが、N-V-A というノードが加わるため、そこから先は少し違うものとなる。
N-V-A では、前の対応するノードである N-V からスコアを引き継ぎ、その分を接尾辞ノードである V-A から引いておく。
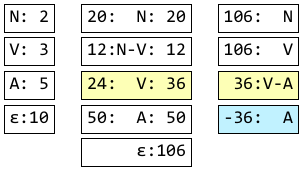
そして、V-A では、V からスコア 36 を引き継ぎ、あらかじめ引かれている分と合わせて 24 になる。接尾辞ノードである A からは、引き継いだスコアである 36 を引いておく。
A では、ε からスコア 106 を引き継ぎ、引かれている分と合わせて 70 になる。
それぞれのノードの重みを掛けると、前向きスコアになる。
3 列目の前向きスコアを合計すると、すべての可能なラベル列の合計スコアである 1330 になっていることがわかる。
後ろ向きスコアは、最初にすべて 1 を割り振るのは上での例と同じ。
それぞれのノードの倍率を掛ける。N-V-A のノードでは、次の 3 つの素性関数が 1 になるため、重みはそれらを掛け合わせた 7.5 になる。
- 文脈にかかわらず、今の位置でラベルが "A" の時に 1 になるもの。重みは 5。
- ある位置の単語が "like" であり、その前の位置のラベルが "V" で、今の位置のラベルが "A" である時に 1 になるもの。重みは 3。
- ある位置の単語が "like" であり、その前の前の位置のラベルが "N" で、前の位置のラベルが "V" で、今の位置のラベルが "A" である時に 1 になるもの。重みは 0.5。
2 列目の差分スコアを求めるため、3 列目のそれぞれのノードについて、自分のスコアと接尾辞ノードのスコアの差分を対応する左ノードに入れていく。
まず、A について。対応する左ノードである ε にスコアを足す。
V-A では、自分のスコアである 15 と、接尾辞ノードのスコアである 5 の差分である 10 を 2 列目の V に入れる。
N-V-A では、自分のスコアである 7.5 と、接尾辞ノードのスコアである 15 の差分である -7.5 を 2 列目の N-V に入れる。ここではマイナスの値になる。
N, V はどちらも ε に入る。ここでは 2 ステップ分を一度に示す。
そして、ε から順に、接尾辞ノードの合計スコアと自分の差分スコアを足したものを自分の合計スコアとする。
たとえば、N-V の接尾辞ノード V のスコアは 20 なので、それに自分の差分スコアである 7.5 を足して、合計スコアは 12.5 になる。
すべて計算すると、次のようになる。
それぞれのノードの重みを掛ける。ε は前につながらないので計算しない。
1 列目の過程は、最初の例と同じようなものなので省略。
結果としては、1 列目の差分スコア(右)と合計スコア(左)は次のようになる。
そして、すべてのノードについて、前向き差分スコアと後ろ向き合計スコアを掛けたものは以下の通り。後ろ向きスコアは、ノードの倍率を掛ける前のもの。
最後に、それぞれのノードのスコアを接尾辞ノードに足し込む。
それぞれの素性関数のスコアは次のようになる。
- 文脈にかかわらず、今の位置でラベルが "N" の時に 1 になるもの: 290+200+212=702
- 文脈にかかわらず、今の位置でラベルが "V" の時に 1 になるもの: 390+630+318=1338
- 文脈にかかわらず、今の位置でラベルが "A" の時に 1 になるもの: 650+500+800=1950
- ある位置の単語が "es" で終わり、その前の位置のラベルが "N" で、今の位置のラベルが "V" である時に 1 になるもの: 150
- ある位置の単語が "like" であり、その前の位置のラベルが "V" で、今の位置のラベルが "A" である時に 1 になるもの: 450
- ある位置の単語が "like" であり、その前の前の位置のラベルが "N" で、前の位置のラベルが "V" で、今の位置のラベルが "A" である時に 1 になるもの: 90
この結果は、すべてのラベル列にわたって計算した結果と一致する。
このように、高次の素性がある場合でも、それによって計算量が急に増えるということはない。
合計・差分アルゴリズムの実装は https://github.com/hiroshi-manabe/crfsuite-variableorder に、きっちりした説明は http://vocrf.net/docs/thesis_en.pdf に書いた。
次に、対比のために一般的な前向き・後ろ向きアルゴリズムで同じ計算をする場合について見てみる。